TD学習#

TD (Temporal difference) learningにおいて，報酬予測誤差(reward prediction error, RPE) \(\delta_{i}\)は次のように計算される．

\[ \delta_{i}=r+\gamma V_{j}\left(x^{\prime}\right)-V_{i}(x) \]

ただし，現在の状態を\(x\), 次の状態を\(x'\), 予測価値分布を\(V(x)\), 報酬信号を\(r\), 時間割引率(time discount)を\(\gamma\)としました． また，\(V_{j}\left(x^{\prime}\right)\)は予測価値分布\(V\left(x^{\prime}\right)\)からのサンプルです． このRPEは脳内において主に中脳のVTA(腹側被蓋野)やSNc(黒質緻密部)におけるドパミン(dopamine)ニューロンの発火率として表現されています．

ただし，VTAとSNcのドパミンニューロンの役割は同一ではありません．ドパミンニューロンへの入力が異なっています (Watabe-Uchida et al., Neuron. 2012)． また，細かいですがドパミンニューロンの発火は報酬量に対して線形ではなく，やや飽和する非線形な応答関数 (Hill functionで近似可能)を持ちます(Eshel et al., Nat. Neurosci. 2016)．このため著者実装では報酬 \(r\)に非線形関数がかかっているものもあります．

先ほどRPEはドパミンニューロンの発火率で表現されている，といいました．RPEが正の場合はドパミンニューロンの発火で表現できますが，単純に考えると負の発火率というものはないため，負のRPEは表現できないように思います．ではどうしているかというと，RPEが0（予想通りの報酬が得られた場合）でもドパミンニューロンは発火しており，RPEが正の場合にはベースラインよりも発火率が上がるようになっています．逆にRPEが負の場合にはベースラインよりも発火率が減少する(抑制される)ようになっています (Schultz et al., Science. 1997; Chang et al., Nat Neurosci. 2016)．発火率というのを言い換えればISI (inter-spike interval, 発火間隔)の長さによってPREが符号化されている(ISIが短いと正のRPE, ISIが長いと負のRPEを表現)ともいえます (Bayer et al., J. Neurophysiol. 2007)．

予測価値(分布) \(V(x)\)ですが，これは線条体(striatum)のパッチ (SNcに抑制性の投射をする)やVTAのGABAニューロン (VTAのドパミンニューロンに投射して減算抑制をする, (Eshel, et al., Nature. 2015))などにおいて表現されている． この予測価値は通常のTD learningでは次式により更新されます．

\[ V_{i}(x) \leftarrow V_{i}(x)+\alpha_{i} f\left(\delta_{i}\right) \]

ただし，\(\alpha_{i}\)は学習率(learning rate), \(f(\cdot)\)はRPEに対する応答関数である．生理学的には\(f(\delta)=\delta\)を使うのが妥当である．

TD誤差

\[ \begin{align} \delta_{t} = r_{t+1} + \gamma V(s_{t+1}) - V(s_{t}) \end{align} \]

価値の更新

\[ \begin{align} V(s_{t}) \leftarrow V(s_{t}) + \alpha \delta_{t} \end{align} \]

(Schultz, Dayan & Montague, Science, 1997)を参考にシミュレーションを行う．60試行する．0秒の時に条件刺激(光刺激)が入る．また，6試行目から40試行目まで条件刺激があってから1.2秒後に報酬が与えられるとする．

using PyPlot
rc("axes.spines", top=false, right=false)

num_trial = 60 # 試行回数
T = 3.0f0 # s
dt = 0.1f0 # s
nt = UInt(T/dt) + 1 # number of timesteps
value = zeros(num_trial, nt) 
delta = zeros(num_trial, nt) # TD error

flash_time = UInt(1.1f0/dt)
delay = UInt(1.2f0/dt)
reward_trial = 6:40 # 報酬が貰える試行の区間を設定する
reward = zeros(num_trial, nt)
reward[reward_trial, flash_time+delay] .= 1.0

α = 0.8 # 学習率
γ = 0.99 # 割引率

# simulation
for i in 2:num_trial
    for t in 1:nt-1
        delta[i, t] = reward[i, t] + γ*value[i-1, t+1] - value[i-1, t]
        if t > flash_time
            value[i, t] = value[i-1, t] + α*delta[i, t]
        end
    end
end

結果を描画する．

figure(figsize=(8, 3.5))

subplot2grid((3,3), (0,0), rowspan=3)
imshow(value); colorbar()
title("Value"); ylabel("Trial"); xlabel("Time (s)"); xticks(0:Int(1/dt):nt, -1:1:T-1)

subplot2grid((3,3), (0,1), rowspan=3)
imshow(delta); colorbar()
title("TD error"); ylabel("Trial"); xlabel("Time (s)"); xticks(0:Int(1/dt):nt, -1:1:T-1)

subplot2grid((3,3), (0,2))
plot(-1:0.1:2, delta[6, :]); title("No CS + R (Trial #6)"); xticks([])

subplot2grid((3,3), (1,2))
plot(-1:0.1:2, delta[30, :]); title("CS + R (Trial #30)"); ylabel("TD error"); xticks([])

subplot2grid((3,3), (2,2))
plot(-1:0.1:2, delta[41, :]); title("CS + No R (Trial #41)"); xlabel("Time (s)")

tight_layout()
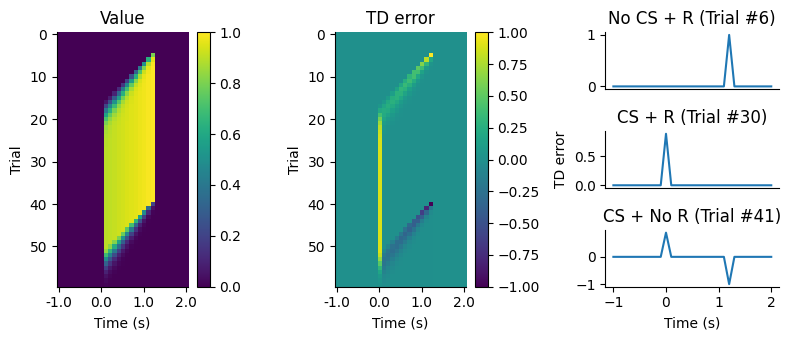
../_images/td-learning_7_0.png

CSは条件刺激(conditioned stimulus), Rは報酬(reward)を意味する．

この際にprediction error信号の時間的変位(temporal shift)が観察されるが，

Rescorla–Wagner model