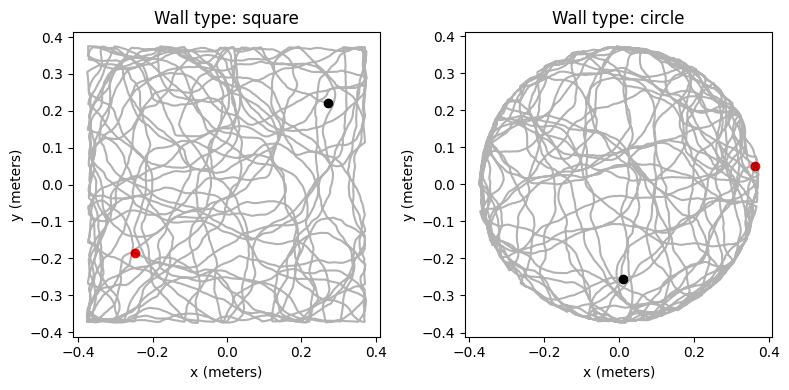
ラット自由行動下の軌跡のシミュレーション

(Raudies & Hasselmo, PLoS Comput Biol. 2012) の擬似コードおよび[https://github.com/ganguli-lab/grid-pattern-formation/blob/master/trajectory_generator.py] を参考に作成．

using PyPlot, LinearAlgebra, Random, Distributions

box_width, box_height = 0.8, 0.8; # Width and height of environment (meters)
perimeter_dist = 0.03  # Perimeter region distance to walls (meters)
σv = 0.13              # Forward velocity Rayleigh distribution scale (m/sec)
μω = 0.0               # Rotation velocity Gaussian distribution mean (rad/sec)
σω = (330 / 360) * 2π  # Rotation velocity Gaussian distribution standard deviation (rad/sec)
dt = 0.02              # Simulation-step time increment (seconds)
decel_rate = 0.25;     # velocity reduction factor when located in the perimeter

Juliaの余りの関数は rem(x, y) と mod(x, y)がある。Juliaのx % yはremと同じだが、Pythonの場合はmodと同じなので、注意。

println("% : ", -1 % 2, ", rem : ", rem(-1, 2), ", mod : ", mod(-1, 2))

% : -1, rem : -1, mod : 1

並進速度をレイリー分布，回転速度を正規分布に従うようにランダムサンプリングする．壁の接ベクトルとラットの距離をdist_wall, 壁の法線ベクトルとラットの頭方向の角度の差をangle_wallとする．なお，壁とはラットの自己速度ベクトルと壁全体との交点である．

• ラットの自己速度ベクトルと壁全体との交点を求める．

• 交点の接ベクトルと法線ベクトルを求める．

• 接ベクトルとの距離をdist_wallとする．

• 法線ベクトルと成す角をangle_wallとする．

function minDistAngle(pos, head_dir, wall_type="square")
    x, y = pos
    if wall_type == "square"
        dists = [box_width/2-x, box_height/2-y, box_width/2+x, box_height/2+y]
        dist_wall, nearest_wall = findmin(dists)
        angle_wall = mod(head_dir - (nearest_wall-1)*π/2 + π, 2π) - π
    elseif wall_type == "circle"
        dist_wall = box_width/2 - sqrt(x^2 + y^2)
        angle_wall = mod(head_dir - atan(y, x) + π, 2π) - π
    end 
    return dist_wall, angle_wall
end;

function generate_trajectory(num_steps, wall_type)
    # store arrays
    position, velocity = zeros(num_steps, 2), zeros(num_steps, 2)
    head_dir = zeros(num_steps) # head direction
    speed = rand(Rayleigh(σv), num_steps) # Forward speed
    random_turn = rand(Normal(μω, σω), num_steps) * dt

    # initial values
    head_dir[1] = rand() * 2π
    position[1, :] = (rand(2) .-0.5) .* ([box_width, box_height] .- perimeter_dist)
    
    # iteration of trajectory
    for t in 1:num_steps-1
        turn_angle = random_turn[t]
        dist_wall, angle_wall = minDistAngle(position[t, :], head_dir[t], wall_type)
        if (dist_wall < perimeter_dist) && (abs(angle_wall) < π/2) # avoid wall
            speed[t] *= decel_rate # deceleration
            turn_angle += sign(angle_wall) * (π/2 - abs(angle_wall))
        end
        velocity[t, :] = speed[t] * [cos(head_dir[t]), sin(head_dir[t])]
        position[t+1, :] = position[t, :] + velocity[t, :] * dt
        head_dir[t+1] = mod(head_dir[t] + turn_angle, 2π) # turn, 
    end
    return position, velocity, speed, head_dir
end;

5分間のシミュレーションを行う．

T = 300 # simulation time (sec)
num_steps = round(Int, T/dt)
wall_types = ["square", "circle"]
positions = zeros(2, num_steps, 2)
for i in 1:2
    positions[i, :, :], _, _, _ =  generate_trajectory(num_steps, wall_types[i]);
end

黒点から始まり、赤点に終わる。

figure(figsize=(8, 4))
for i in 1:2
    subplot(1,2,i)
    title("Wall type: "*wall_types[i])
    xlabel("x (meters)"); ylabel("y (meters)")
    plot(positions[i, 1, 1], positions[i, 1, 2], "ko", label="Start")
    plot(positions[i, end, 1], positions[i, end, 2], "ro", label="Goal")
    plot(positions[i, :, 1], positions[i, :, 2], color="k", alpha=0.3)
end
tight_layout()