無限時間最適フィードバック制御モデル#

モデルの構造#

無限時間最適フィードバック制御モデル (infinite-horizon optimal feedback control model) [Qian et al., 2013]

\[\begin{split} \begin{array}{l} d x=(\mathbf{A} x+\mathbf{B} u) dt +\mathbf{Y} u d \gamma+\mathbf{G} d \omega \\ d y=\mathbf{C} x dt+\mathbf{D} d \xi\\ d \hat{x}=(\mathbf{A} \hat{x}+\mathbf{B} u) dt+\mathbf{K}(dy-\mathbf{C} \hat{x} dt) \end{array} \end{split}\]

実装#

ライブラリの読み込みと関数の定義．

using Base: @kwdef
using Parameters: @unpack
using LinearAlgebra, Kronecker, Random, BlockDiagonals, PyPlot
rc("axes.spines", top=false, right=false)
rc("font", family="Arial")

定数の定義

\[\begin{split} \begin{aligned} \alpha_{1}&=\frac{b}{t_{a} t_{e} I},\quad \alpha_{2}=\frac{1}{t_{a} t_{e}}+\left(\frac{1}{t_{a}}+\frac{1}{t_{e}}\right) \frac{b}{I} \\ \alpha_{3}&=\frac{b}{I}+\frac{1}{t_{a}}+\frac{1}{t_{e}},\quad b_{u}=\frac{1}{t_{a} t_{e} I} \end{aligned} \end{split}\]
@kwdef struct SaccadeModelParameter
    n = 4 # number of dims
    i = 0.25 # kgm^2, 
    b = 0.2 # kgm^2/s
    ta = 0.03 # s
    te = 0.04 # s
    L0 = 0.35 # m

    bu = 1 / (ta * te * i)
    α1 = bu * b
    α2 = 1/(ta * te) + (1/ta + 1/te) * b/i
    α3 = b/i + 1/ta + 1/te

    A = [zeros(3) I(3); -[0, α1, α2, α3]']
    B = [zeros(3); bu]
    C = [I(3) zeros(3)]
    D = Diagonal([1e-3, 1e-2, 5e-2])

    Y = 0.02 * B
    G = 0.03 * I(n)

    Q = Diagonal([1.0, 0.01, 0, 0]) 
    R = 0.0001
    U = Diagonal([1.0, 0.1, 0.01, 0])
end

SaccadeModelParameter
\[\begin{split} \begin{array}{l} \mathbf{X}:=\left[\begin{array}{l} x \\ \tilde{x} \end{array}\right], d \bar{\omega} :=\left[\begin{array}{c} d \omega \\ d \xi \end{array}\right], \bar{\mathbf{A}} :=\left[\begin{array}{cc} \mathbf{A}-\mathbf{B} \mathbf{L} & \mathbf{B} \mathbf{L} \\ \mathbf{0} & \mathbf{A}-\mathbf{K} \mathbf{C} \end{array}\right] \\ \bar{\mathbf{Y}} :=\left[\begin{array}{cc} -\mathbf{Y} \mathbf{L} & \mathbf{Y} \mathbf{L} \\ -\mathbf{Y} \mathbf{L} & \mathbf{Y} \mathbf{L} \end{array}\right], \bar{G} :=\left[\begin{array}{cc} \mathbf{G} & \mathbf{0} \\ \mathbf{G} & -\mathbf{K} \mathbf{D} \end{array}\right] \end{array} \end{split}\]

とする．元論文では\(F, \bar{F}\)が定義されていたが，\(F=0\)とするため，以後の式から削除した．

\[\begin{split} \begin{array}{l} \mathbf{P} :=\left[\begin{array}{cc} \mathbf{P}_{11} & \mathbf{P}_{12} \\ \mathbf{P}_{12} & \mathbf{P}_{22} \end{array}\right] := E\left[\mathbf{X} \mathbf{X}^\top\right] \\ \mathbf{V} :=\left[\begin{array}{cc} \mathbf{Q}+\mathbf{L}^\top R \mathbf{L} & -\mathbf{L}^\top R \mathbf{L} \\ -\mathbf{L}^\top R \mathbf{L} & \mathbf{L}^\top R \mathbf{L}+\mathbf{U} \end{array}\right] \end{array} \end{split}\]
\[\begin{split} \begin{align} &K=\mathbf{P}_{22} \mathbf{C}^\top\left(\mathbf{D} \mathbf{D}^\top\right)^{-1} \\ &\mathbf{L}=\left(R+\mathbf{Y}^\top\left(\mathbf{S}_{11}+\mathbf{S}_{22}\right) \mathbf{Y}\right)^{-1} \mathbf{B}^\top \mathbf{S}_{11} \\ &\bar{\mathbf{A}}^\top \mathbf{S}+\mathbf{S} \bar{\mathbf{A}}+\bar{\mathbf{Y}}^\top \mathbf{S} \bar{\mathbf{Y}}+\mathbf{V}=0 \\ &\bar{\mathbf{A}} \mathbf{P}+\mathbf{P} \bar{\mathbf{A}}^\top+\bar{\mathbf{Y}} \mathbf{P} \bar{\mathbf{Y}}^\top+\bar{\mathbf{G}} \bar{\mathbf{G}}^\top=0 \end{align} \end{split}\]

\(\mathbf{A} = (a_{ij})\) を \(m \times n\) 行列，\(\mathbf{B} = (b_{kl})\) を \(p \times q\) 行列とすると、それらのクロネッカー積 \(\mathbf{A} \otimes \mathbf{B}\) は

\[\begin{split} \mathbf{A}\otimes \mathbf{B}={\begin{bmatrix}a_{11}\mathbf{B}&\cdots &a_{1n}\mathbf{B}\\\vdots &\ddots &\vdots \\a_{m1}\mathbf{B}&\cdots &a_{mn}\mathbf{B}\end{bmatrix}} \end{split}\]

で与えられる \(mp \times nq\) 区分行列である．

Roth’s column lemma (vec-trick)

\[ (\mathbf{B}^\top \otimes \mathbf{A})\text{vec}(\mathbf{X}) = \text{vec}(\mathbf{A}\mathbf{X}\mathbf{B})=\text{vec}(\mathbf{C}) \]

によりこれを解くと，

\[\begin{split} \begin{align} \mathbf{S} &= -\text{vec}^{-1}\left(\left(\mathbf{I} \otimes \bar{\mathbf{A}}^\top + \bar{\mathbf{A}}^\top \otimes \mathbf{I} + \bar{\mathbf{Y}}^\top \otimes \bar{\mathbf{Y}}^\top\right)^{-1}\text{vec}(\mathbf{V})\right)\\ \mathbf{P} &= -\text{vec}^{-1}\left(\left(\mathbf{I} \otimes \bar{\mathbf{A}} + \bar{\mathbf{A}} \otimes \mathbf{I} + \bar{\mathbf{Y}} \otimes \bar{\mathbf{Y}}\right)^{-1}\text{vec}(\bar{\mathbf{G}}\bar{\mathbf{G}}^\top)\right) \end{align} \end{split}\]

となる．ここで\(\mathbf{I}=\mathbf{I}^\top\)を用いた．

K, L, S, Pの計算#

  1. LとKをランダムに初期化

  2. SとPを計算

  3. LとKを更新

  4. 収束するまで2と3を繰り返す．

収束スピードはかなり速い．

function infinite_horizon_ofc(param::SaccadeModelParameter, maxiter=1000, ϵ=1e-8)
    @unpack n, A, B, C, D, Y, G, Q, R, U = param
    
    # initialize
    L = rand(n)' # Feedback gains
    K = rand(n, 3) # Kalman gains
    I₂ₙ = I(2n)

    for _ in 1:maxiter
        Ā = [A-B*L B*L; zeros(size(A)) (A-K*C)]
        Ȳ = [-ones(2) ones(2)] ⊗ (Y*L) 
        Ḡ = [G zeros(size(K)); G (-K*D)]
        V = BlockDiagonal([Q, U]) + [1 -1; -1 1] ⊗ (L'* R * L)

        # update S, P
        S = -reshape((I₂ₙ ⊗ (Ā)' +  (Ā)' ⊗ I₂ₙ + (Ȳ)' ⊗ (Ȳ)') \ vec(V), (2n, 2n))
        P = -reshape((I₂ₙ ⊗ Ā +  Ā ⊗ I₂ₙ + Ȳ ⊗  Ȳ) \ vec(Ḡ * (Ḡ)'), (2n, 2n))

        # update K, L
        P₂₂ = P[n+1:2n, n+1:2n]
        S₁₁ = S[1:n, 1:n]
        S₂₂ = S[n+1:2n, n+1:2n]

        Kₜ₋₁ = copy(K)
        Lₜ₋₁ = copy(L)

        K = P₂₂ * C' / (D * D')
        L = (R + Y' * (S₁₁ + S₂₂) * Y) \ B' * S₁₁
        if sum(abs.(K - Kₜ₋₁)) < ϵ && sum(abs.(L - Lₜ₋₁)) < ϵ
            break
        end
    end
    return L, K
end

infinite_horizon_ofc (generic function with 3 methods)

param = SaccadeModelParameter()
L, K = infinite_horizon_ofc(param);

シミュレーション#

function simulation(param::SaccadeModelParameter, L, K, dt=0.001, T=2.0, init_pos=-0.5; noisy=true)
    @unpack n, A, B, C, D, Y, G, Q, R, U = param
    nt = round(Int, T/dt)
    X = zeros(n, nt)
    u = zeros(nt)
    X[1, 1] = init_pos # m; initial position (target position is zero)

    if noisy
        sqrtdt = √dt
        X̂ = zeros(n, nt)
        X̂[1, 1] = X[1, 1]
        for t in 1:nt-1
            u[t] = -L * X̂[:, t]
            X[:, t+1] = X[:,t] + (A * X[:,t] + B * u[t]) * dt + sqrtdt * (Y * u[t] * randn() + G * randn(n))
            dy = C * X[:,t] * dt + D * sqrtdt * randn(n-1)
            X̂[:, t+1] = X̂[:,t] + (A * X̂[:,t] + B * u[t]) * dt + K * (dy - C * X̂[:,t] * dt)
        end
    else
        for t in 1:nt-1
            u[t] = -L * X[:, t]
            X[:, t+1] = X[:, t] + (A * X[:, t] + B * u[t]) * dt
        end
    end
    return X, u
end

simulation (generic function with 4 methods)

理想状況でのシミュレーション

dt = 1e-3
T = 1.0

1.0

Xa, ua = simulation(param, L, K, dt, T, noisy=false);

ノイズを含むシミュレーション#

n = 4
nsim = 10
XSimAll = []
uSimAll = []
for i in 1:nsim
    XSim, u = simulation(param, L, K, dt, T, noisy=true);
    push!(XSimAll, XSim)
    push!(uSimAll, u)
end

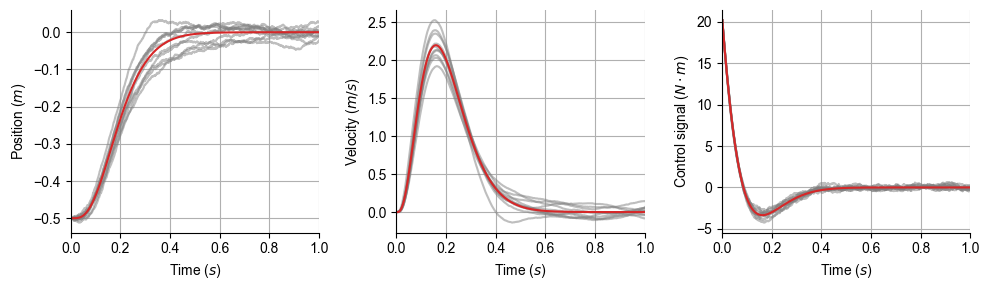
結果の描画#

tarray = collect(dt:dt:T)
label = [L"Position ($m$)", L"Velocity ($m/s$)", L"Acceleration ($m/s^2$)", L"Jerk ($m/s^3$)"]

fig, ax = subplots(1, 3, figsize=(10, 3))
for i in 1:2
    for j in 1:nsim
        ax[i].plot(tarray, XSimAll[j][i,:]', "tab:gray", alpha=0.5)
    end
    
    ax[i].plot(tarray, Xa[i,:], "tab:red")
    ax[i].set_ylabel(label[i]); ax[i].set_xlabel(L"Time ($s$)"); ax[i].set_xlim(0, T); ax[i].grid()
end

for j in 1:nsim
    ax[3].plot(tarray, uSimAll[j], "tab:gray", alpha=0.5)
end
ax[3].plot(tarray, ua, "tab:red")
ax[3].set_ylabel(L"Control signal ($N\cdot m$)"); ax[3].set_xlabel(L"Time ($s$)"); ax[3].set_xlim(0, T); ax[3].grid()

tight_layout()
../_images/infinite-horizon-ofc_21_0.png

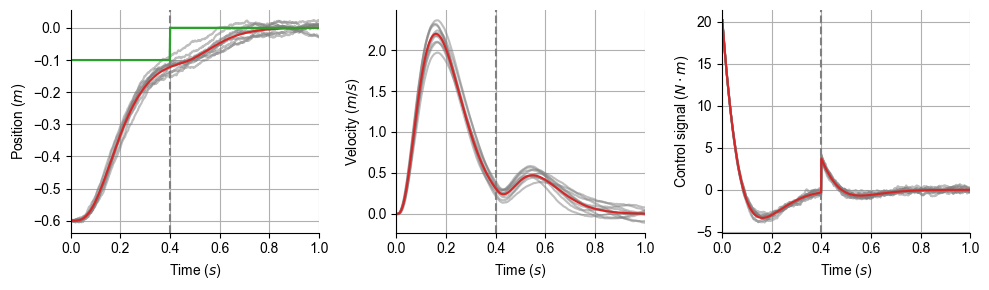
Target jump#

target jumpする場合の最適制御 [Li et al., 2018]

function target_jump_simulation(param::SaccadeModelParameter, L, K, dt=0.001, T=2.0, 
        Ttj=0.4, tj_dist=0.1, 
        init_pos=-0.5; noisy=true)
    # Ttj : target jumping timing (sec)
    # tj_dist : target jump distance
    @unpack n, A, B, C, D, Y, G, Q, R, U = param
    nt = round(Int, T/dt)
    ntj = round(Int, Ttj/dt)
    X = zeros(n, nt)
    u = zeros(nt)
    X[1, 1] = init_pos # m; initial position (target position is zero)

    if noisy
        sqrtdt = √dt
        X̂ = zeros(n, nt)
        X̂[1, 1] = X[1, 1]
        for t in 1:nt-1
            if t == ntj
                X[1, t] -= tj_dist # When k == ntj, target jumpさせる（実際には現在の位置をずらす）
                X̂[1, t] -= tj_dist
            end
            u[t] = -L * X̂[:, t]
            X[:, t+1] = X[:,t] + (A * X[:,t] + B * u[t]) * dt + sqrtdt * (Y * u[t] * randn() + G * randn(n))
            dy = C * X[:,t] * dt + D * sqrtdt * randn(n-1)
            X̂[:, t+1] = X̂[:,t] + (A * X̂[:,t] + B * u[t]) * dt + K * (dy - C * X̂[:,t] * dt)
        end
    else
        for t in 1:nt-1
            if t == ntj
                X[1, t] -= tj_dist # When k == ntj, target jumpさせる（実際には現在の位置をずらす）
            end
            u[t] = -L * X[:, t]
            X[:, t+1] = X[:, t] + (A * X[:, t] + B * u[t]) * dt
        end
    end
    X[1, 1:ntj-1] .-= tj_dist;
    return X, u
end

target_jump_simulation (generic function with 6 methods)

Ttj = 0.4
tj_dist = 0.1
nt = round(Int, T/dt)
ntj = round(Int, Ttj/dt);

Xtj, utj = target_jump_simulation(param, L, K, dt, T, noisy=false);

XtjAll = []
utjAll = []
for i in 1:nsim
    XSim, u = target_jump_simulation(param, L, K, dt, T, noisy=true);
    push!(XtjAll, XSim)
    push!(utjAll, u)
end

target_pos = zeros(nt)
target_pos[1:ntj-1] .-= tj_dist; 

fig, ax = subplots(1, 3, figsize=(10, 3))
for i in 1:2
    ax[1].plot(tarray, target_pos, "tab:green")
    for j in 1:nsim
        ax[i].plot(tarray, XtjAll[j][i,:]', "tab:gray", alpha=0.5)
    end
    ax[i].axvline(x=Ttj, color="gray", linestyle="dashed")
    ax[i].plot(tarray, Xtj[i,:], "tab:red")
    ax[i].set_ylabel(label[i]); ax[i].set_xlabel(L"Time ($s$)"); ax[i].set_xlim(0, T); ax[i].grid()
end
for j in 1:nsim
    ax[3].plot(tarray, utjAll[j], "tab:gray", alpha=0.5)
end
ax[3].axvline(x=Ttj, color="gray", linestyle="dashed")
ax[3].plot(tarray, utj, "tab:red")
ax[3].set_ylabel(L"Control signal ($N\cdot m$)"); ax[3].set_xlabel(L"Time ($s$)"); ax[3].set_xlim(0, T); ax[3].grid()

tight_layout()
../_images/infinite-horizon-ofc_27_0.png

参考文献#

LMSQ18

Zhe Li, Pietro Mazzoni, Sen Song, and Ning Qian. A single, continuously applied control policy for modeling reaching movements with and without perturbation. Neural Comput., 30(2):397–427, February 2018.

QJJM13

Ning Qian, Yu Jiang, Zhong-Ping Jiang, and Pietro Mazzoni. Movement duration, fitts's law, and an infinite-horizon optimal feedback control model for biological motor systems. Neural Comput., 25(3):697–724, March 2013.